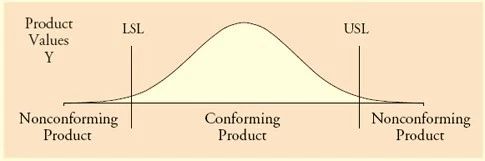
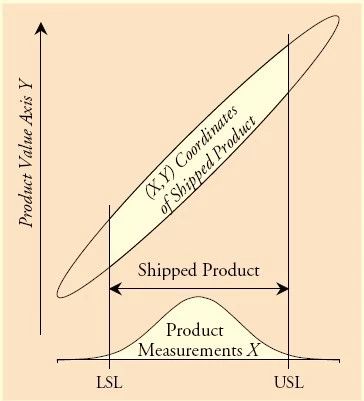
产品的合格标准已知,上下限的规格值也已经给出,如上图的LSL与USL。在LSL与USL之间的产品将是合格产品。
但是实际的Y值我们是不知道的,需要用测量系统去测量它,Y的测量值我们称之为X。
测量出来的X值是不等于Y的,因为有测量误差的存在,这个误差我们称之为E。因为测量误差也是正态分布,因此我们得出测量值的分布如下图,与Y的分布形状类似,但是X的方差要大一些,等于Y的方差加上测量误差E的方差。
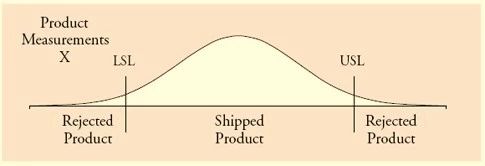
接下来我们用双变量正态分布来显示Y与X的相关性。
该分布的概率模型可以在XY坐标平面中由一系列椭圆表示,下图显示了两个双变量正态分布的一,二和三标准偏差等值线,其中组内相关系数分别为设定为0.95和0.80。
从上图可以看到,随着测量误差的增加,双变量正态分布的椭圆变得更胖,主轴线偏斜。
我们感兴趣的是:哪个范围内的测量值X对应的是合格的Y。
下图白色范围标示出了合格产品的范围。

而下面这张图标示出来了100%检验后出货的产品的范围。
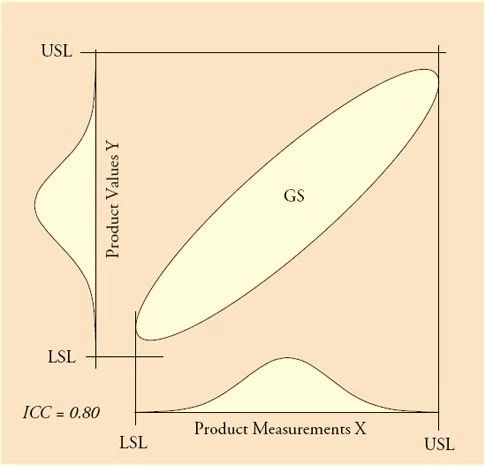
到此,我们已经很清楚地看到,100%检验后出货产品的范围与实际合格产品的范围是不同的。
100%检验通过的产品范围 ≠ 合格产品的范围
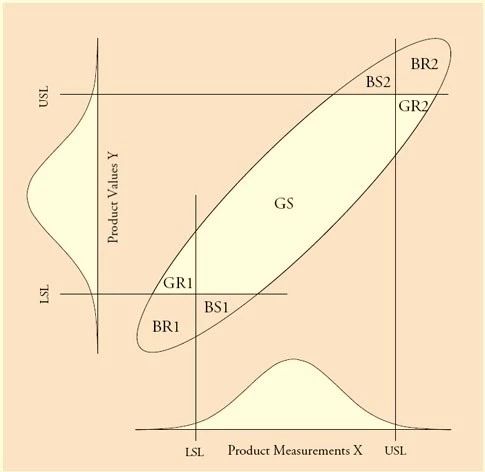
我们用产品的合格好坏与出货与否将所有产品分为四个类别:
合格的检验通过的产品(GS:Good and Shipped)
合格的检验拒收的产品(GR:Good and Rejected)
不合格的检验通过的产品(BS:Bad and Shipped)
不合格的检验拒收的产品(BR:Bad and Rejected)
GS与BR是我们想看到的结果,BS将给客户带来麻烦,而GR将给自己带来麻烦。
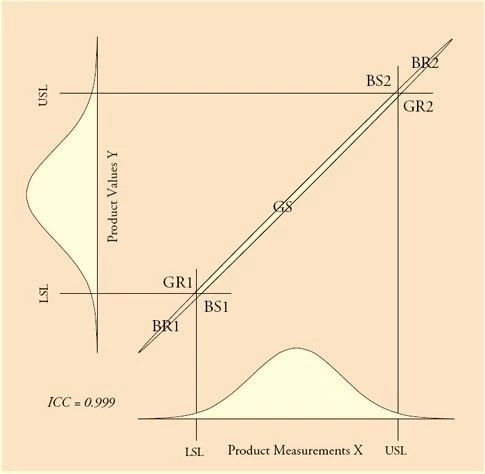
下图显示了各个类别在双变量正态分布中的位置。
对于生产者来说,他希望的是合格产品的出货比例(PGS: Proportion of good product that is shipped)尽可能的高:
PGS = GS / (GS + GR1 + GR2)
对于客户来说,他希望的则是不良产品被拒收的比例(PBR: Proportion of bad product that is rejected)尽可能的高:
PBR = (BR1 + BR2) / (BR1 + BR2 + BS1 + BS2)
糟糕的是,PGS与PBR二者并不是线性相关的。
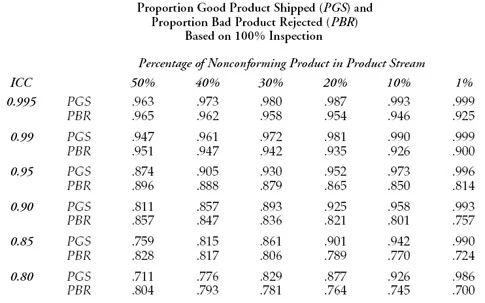
下面是一个评估表,呈现了在不同的测量误差水平,总体不合格产品比例情况下,PGS与PBR的值。

就以上表中最右下角的一组数据来做解读:当整体产品的不合格率在1%,测量误差较大(ICC = 0.8)时,生产者将有98.6%的概率将合格品出货,但是不良产品拒收的比例只有70%,大量的不良品将流向客户。
怎么解决这个问题呢?似乎只有两种办法。
第一种办法:坚持100%检验,那么就要改进测量系统,使得双变量正态分布中的椭圆扁到像一条直线一样,这时PGS与PBR都会非常高。
代价是:你需要一个趋近完美的测量系统,这往往需要巨大的投资,同时巨大的投资并没有解决问题,而只是把问题留了下来。
第二种办法:提升过程能力,使得过程的产出都在规格上下限范围内,这时候已经不需要100%检验了,既可以节省升级测试系统的投资,又可以省去检验的花费,更关键的是真正解决了问题。
至此,我们的结论已经非常清晰:
测量系统误差的存在,使得100%检验无法具备100%的有效性;
100%检验解决不了质量问题,还会需要不必要的设备投资与人员检验费用;
测量系统应该被用来实质上改善生产过程的质量和一致性,而不是用来做检验。














